
Market Risk Measurement
Market risks can and should be measured continuously to avoid unexpected losts.
When properly understood, risk controls can be integrated to the portfolio construction process which leads to superior Return / Risk ratios.
What's New:
More Educational Content coming soon
 More educational content
to come. Sujects include double taxation of bonds and corporate governance.
More educational content
to come. Sujects include double taxation of bonds and corporate governance.
April 19, 2012: Death of a great investment counselor, Carl H. Otto
Updated: April 20, 2012
Risk Measurement and Monitoring
Introduction
I once presented to a potential client who told me a story about an investment manager he hired and fired back 6 months later because he had underperformed by 20%. That investor clearly did not measure the manager’s active risk before hiring him.
ClermontAlpha – Risk-Controlled Alpha Expert, Hedge Funds & Fund of Funds
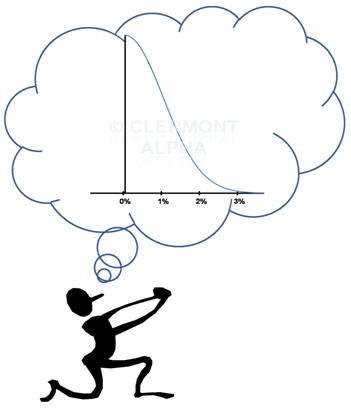
We all dream about asymmetric active return with a positive skew – or even better: we wish we can only get the right side of any expected active return distribution. Some say that they want to take a lot more risk as long as their manager delivers on the right side of that distribution… Stop dreaming. Active returns tend to have two sides to its distribution!
When looking at hiring an investment manager, the difficulty is to quantify beforehand what is the expected risk-return profile of that manager. The expected active return is very difficult to define as it GENERALLY takes well over 16 years to be 95% confident that the value added is significantly different from 0. On the other hand, the active risk is easy to estimate as it is a function of each stock’s weight in the portfolio, each stock’s variance and all their covariances with all other stocks.
Estimating Risk
The risk of any portfolios, whether traditional long only or long-short, is very easy to estimate. For any portfolio, the total risk is:
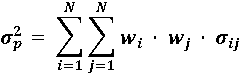
Where:
wi = Weight of stock i in the portfolio p
σij = Covariance of stock i with stock j
σii = σi2 = Variance of stock i
In matrix form, the equation can be written as:

For an estimate of active risk (vs a benchmark) or expected tracking error, we replace weights in the above equation by the active weights vs the benchmark. The rest of the mathematics is the same:

Curse of Dimensionality
The number of variances and covariances to estimate can be quite large. For example, with a universe of 1,000 stocks, we need to estimate 1,000 variances, and 499,500 covariances. This is much more parameters to estimate than data points to be used in the estimate. This problem is referred to, in the academic literature, as the curse of dimensionality.
The approach used to solve this problem is to find a series of common factors that explain stocks returns as in:
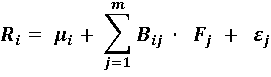
Where:
Ri = Return of stock i
Bij = Sensitivity or exposure of stock I to factor j
Fj = Return to factor j
εi = Stock specific return
Multiple Factor Models
There are three main categories of Factor Models:
- Macroeconomic factor model (BIRR)
- The Factor returns are known (ex: change in interest rate)
- The exposure to the factors are not known
- Fundamental factor model (BARRA, Northfield, Axioma)
- The factor exposures are known (ex: company size or industry)
- The factor returns are unknown
- Statistical factor model (APT)
- Both the factor exposure and factor return are unknown and are estimated using a statistical technique like Principal Component analysis or Factor analysis.
While each approach has advantages and disadvantages, fundamental factor models have been more widely used because of its predictive ability, ease of understanding (closer to the way investors think), and better portfolio construction.
Over the last decade, we have seen an emergence of risk models which combine two or three of the above approaches and are sometimes referred to as hybrid models (Northfield).
Which type of factor model is best depends on what we want to do. We will always get a better estimate of risk and better portfolio construction with a risk model closely linked to the alpha generation process – something that most market participants don’t fully recognize. Some risk model companies have recently started to adapt their model to reduce the impact of misaligned factors.
Conclusion
Risk measurement is very well understood. While no risk model is perfect, it is preferable to have an imperfect measure of risk than no measure. Personally, I prefer to have numerous measures of risk according to various models – understanding the limitations of each measure.
While most investment managers talk about risk controls in their investment process, many managers still today do not quantify the risk in their portfolios.
If your manager is not monitoring the risk in your portfolio, perhaps you should replace that investment manager.
If your manager is not talking about variances and covariances when talking about risk – or if he talks about how he selects stocks to avoid losses – perhaps you should replace that investment manager.
Dominic Clermont, ASA, MBA, CFA





